로또를 둘러싼 의문
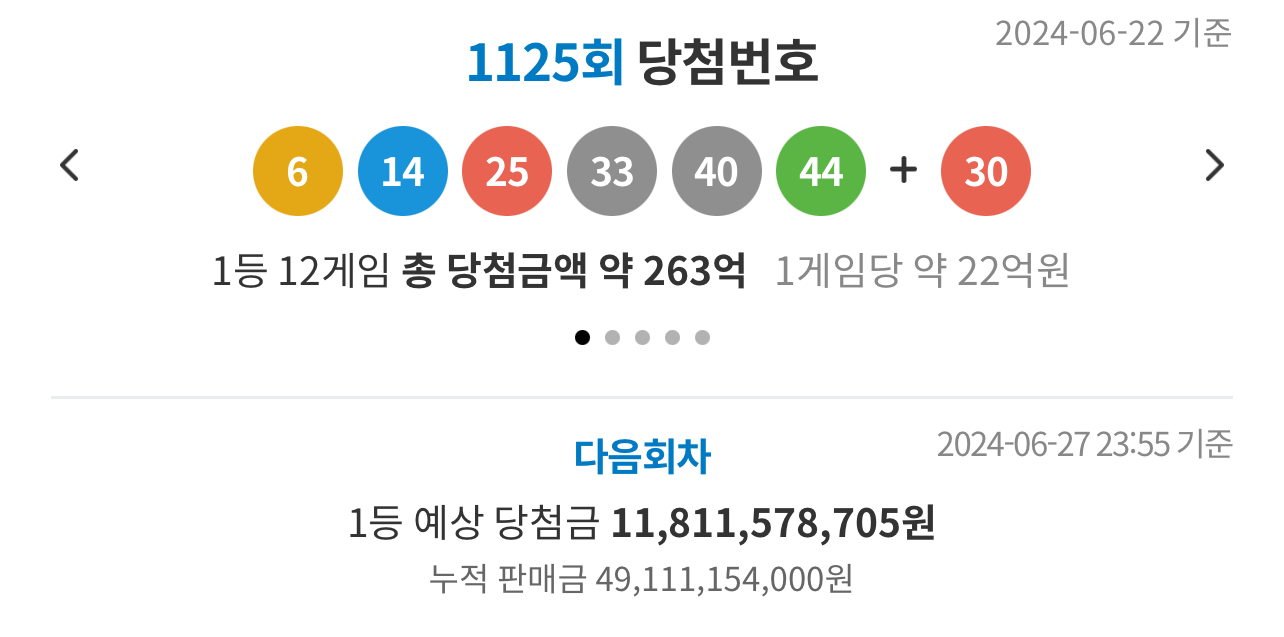
1126회차 누적 판매금이 490억 원을 넘어섰다. 하루 만에 160억 원이 늘어났는데 이 추세라면 이번 회차 당첨금액이 꽤나 쏠쏠하게 나올 듯하다.
궁금증 1. 회차마다 발생하는 다수의 당첨자
로또는 45개의 숫자 중 6개의 숫자를 선택해야 하며, 1등에 당첨될 확률은 1/8,145,060 이다. 만약 n명의 사람들이 독립적으로 로또를 구매한다고 가정하면, 각 사람이 1등에 당첨될 확률은 여전히 1/8,145,060로 동일하다.
각 사람의 당첨 여부를 독립적인 베르누이 시도로 생각해 보자. 계산하고자 하는 것은 n번의 시도 중에서 1등 당첨자가 10명 이상 나올 확률로, 이항 분포를 사용해 접근할 수 있다. 이항 분포에서 성공 확률이 매우 작고 시도 횟수가 매우 많을 때에는 포아송 분포를 근사적으로 사용할 수 있는 것으로 알려져 있으니 파이썬을 활용해 10명 이상 1등에 당첨될 확률을 구해보자.
import scipy.stats as stats
# 총 로또 구매자 수를 천만 명이라고 가정하고
n = 10000000
# 통상적으로 1등에 당첨될 확률 (1 / 8,145,060)
p_win = 1 / 8145060
# 평균적으로 발생할 수 있는 1등 당첨자 수 (λ)
lambda_ = n * p_win
# 10명 이상이 1등에 당첨될 확률 계산
prob_10_or_more = 1 - stats.poisson.cdf(9, lambda_)
# 계산결과
print(f"평균 1등 당첨자 수 (λ): {lambda_:.6f}")
print(f"10명 이상이 1등에 당첨될 확률: {prob_10_or_more:.10f}")그리하여 나온 결과값은?
발생할 수 있는 1등 당첨자 수 (λ): 1.227738명
10명 이상 1등 당첨될 확률: 0.00007062%
물론 이 값은 한 명이 한 게임을 했다고 가정한 것이고 실제로는 10만 원을 꽉 채우는 사람, 5천 원어치만 사는 사람 또는 만 원어치만 사는 사람 등 다양한 유형이 존재하니 이 결과로 단정 짓기에는 무리가 좀 있고,
실제 판매금액을 고려해보면 주당 500~600억 원이니까 천만 명의 사람이 오천 원씩 게임을 즐겼다고 가정한다면 발생할 수 있는 1등 당첨자의 수는 5배인 약 6.1명이 되는 것이고 10명 이상이 1등에 당첨될 확률 또한 1.7%로 대폭(?) 늘어나는 것이니....
그래도 꾸준하게 10명 또는 그 이상의 당첨자가 나오는 확률상 여전히 논란의 여지가 있어보인다.
궁금증 2. 온라인 로또 구매 한도액
동행로또 홈페이지에서는 자주 묻는 질문과 답변을 통해 궁금증을 해결할 수 있도록 자료를 제공해주고 있는데 온라인으로 구매가능한 전자복권의 1일 이용한도를 10만 원이라고 안내하고 있다.

그런데!!

왜 로또는 5천 원만 가능하게 막아둔 것일까? 어디에서도 답변을 찾을 수 없었다. 혹시 이 글을 읽으신 분들 중 이유를 아는 분이 계시다면 답글 좀 남겨주시길....